Imaginez trois octaèdres imbriqués les uns dans les autres, dans les trois directions de l'espace. On obtient une sorte de forme étoilée à 12 pointes. Je l'ai coloriée afin que deux faces contiguës n'aient jamais la même couleur. Voici comment le réaliser. Télécharger le fichier, et l'imprimer deux fois (il faut six pièces en tout. Rainurer et découper, on obtient six pièces semblables à celle-ci :

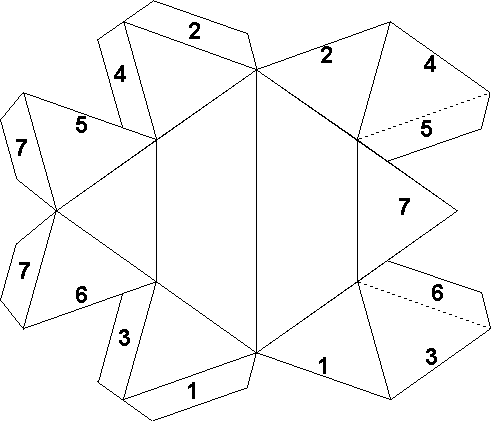
Pour le pliage, attention, il y a deux plis inversés (en creux). Voici un schéma montrant les plis inversés en pointillé, et l'ordre des collages (chaque languette de collage se colle sur la face portant le même numéro).
Plier les six éléments en les préformant pour bien préparer la forme. On obtient ceci (deux fois) :

Ensuite, je réalise un collage à la fois par pièce, puis je passe à la pièce suivante, ça laisse le temps à la colle de bien sécher. On commence par approcher les faces jaunes et vertes (collages 1 et 2), on obtient ceci :

Rabattre et coller les faces blanches (collages 3 et 4). On obtient ceci :

Cette image montre bien un des problèmes de la conception des languettes : les angles des languettes sont théoriques. Si on les coupe exactement avec ces angles, elles ont tendance à se chevaucher à cause de l'épaisseur du papier. Ainsi, je réduit toujours très légèrement l'angle de découpe des languettes de collage (inversement je les découpe souvent un peu plus longues).
Faire un par un les collages 5 et 6, et "fermer la boîte" en collant le dernier triangle (7).
Il vous reste un dernier morceau de bravoure : trouver comment les assembler (sans les écrabouiller sauvagement dans un moment de colère ;-) pour obtenir ceci :

Le tout prend un peu moins d'une heure. Si la forme vous plaît, je peux en poster d'autres : un bleu-blanc-rouge, un autre avec des dessins d'Escher, un tout blanc (qui sert de modèle pour les conceptions). J'ai en projet d'en concevoir d'autres :
-le même mais avec des octaèdres réguliers, donc des triangles exactement équilatéraux ;
-une autre disposition des couleurs, afin qu'il faille rechercher le bon assemblage pour reproduire un modèle (un puzzle en quelque sorte).



